'바닥부터 배우는 강화 학습' 4장에는 MDP를 알고 있는 경우 정책을 발전시키는 플래닝 방법에 대해서 설명하고 있습니다. 아래 내용은 공부하면서 핵심 내용을 정리한 것입니다.
참고자료
- 도서: 바닥부터 배우는 강화 학습 / 4장 MDP를 알 때의 플래닝
- 동영상: https://www.youtube.com/watch?v=rrTxOkbHj-M&t=29s
전제조건
- 다음 두 조건이 만족하는 상황
◦ 작은 문제
◦ MDP를 알 때 - 플래닝(planning): MDP에 대한 모든 정보를 알 때 이를 이용하여 정책을 개선해 나가는 과정
4.1 밸류 평가하기 - 반복적 정책 평가
- 반복적 정책 평가(Iterative policy evaluation) 방법을 통해 각 상태 $s$에 대한 가치 함수 $v(s)$ 계산 가능
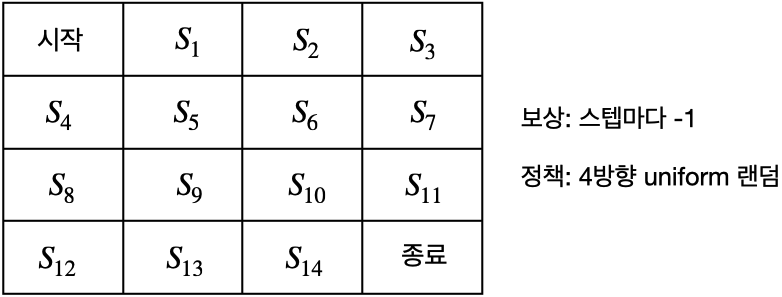
- 위 그림 그리드 월드의 MDP 정보
◦ 모든 상태 $s$에서의 보상: $r_s^a=-1$
◦ 모든 상태 $s$에서의 전이 확률: $P_{ss'}^a=1.0$
◦ 감쇠 인자: $\gamma = 1$
1. 테이블 초기화
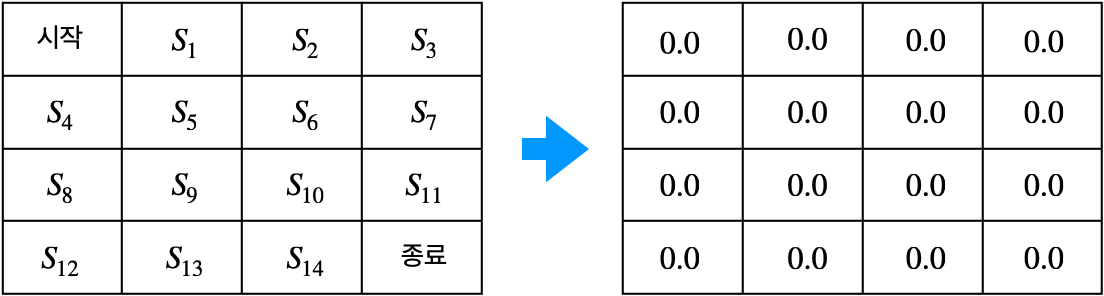
- 모든 상태의 밸류를 0으로 초기화
2. 한 상태의 값을 업데이트
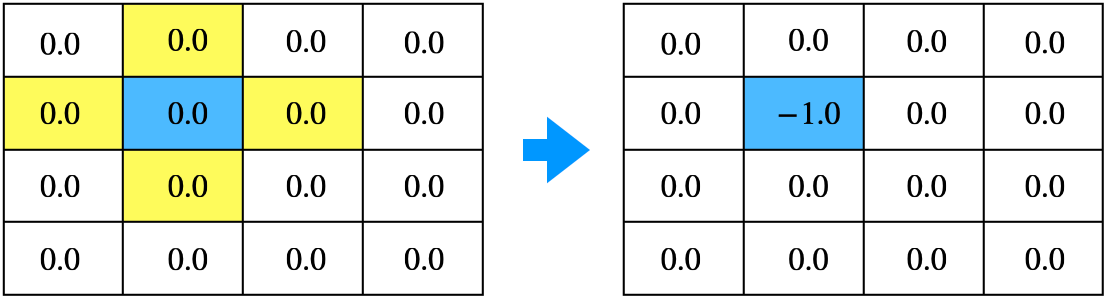
- 2단계 수식 $v_{\pi}(s)=\sum_{a \in A} \pi(a|s) \left( r_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_{\pi}(s') \right)$을 이용해 상태 $s_5$를 업데이트
$$\begin{equation}
\begin{split}
v_{\pi}(s_5) = & 0.25 * (-1 + 0.0) + 0.25 * (-1 + 0.0) + \\
& 0.25 * (-1 + 0.0) + 0.25 * (-1 + 0.0) = -1.0
\end{split}
\end{equation}$$

- 위 수식에서 임의의 값 $v_{\pi}(s')$에 환경이 주는 보상 $r_s^a$를 섞어서 $v_{\pi}(s)$ 계산
- 처음에는 임의의 값이지만 지속적으로 업데이트하면 임의의 값의 영향은 사라지고 실제 값에 가까워짐
3. 모든 상태에 대해 2의 과정을 적용
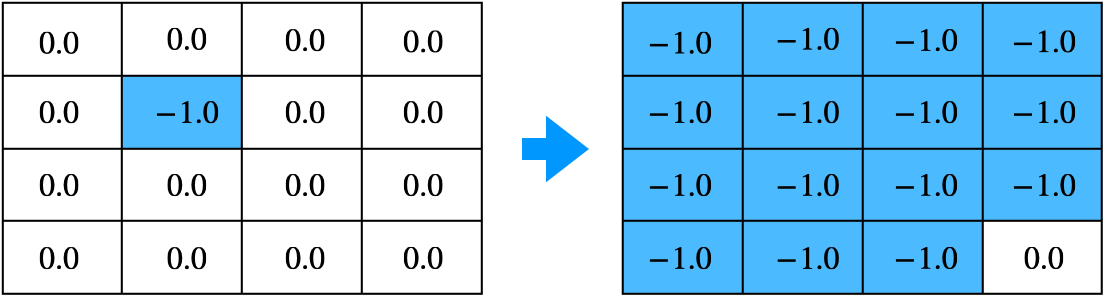
- 이미 업데이트한 상태 $s_5$이외에 모든 상태를 업데이트
4. 앞의 2 ~ 3 과정을 계속해서 반복

- 벨만 기대 방정식을 이용해 업데이트를 계속해서 실제 가치를 알 수 있음
4.2 최고의 정책 찾기 - 정책 이터레이션
- 정책 평가와 정책 개선을 번갈아 수행하여 정책이 수렴할 때까지 반복하는 방법론
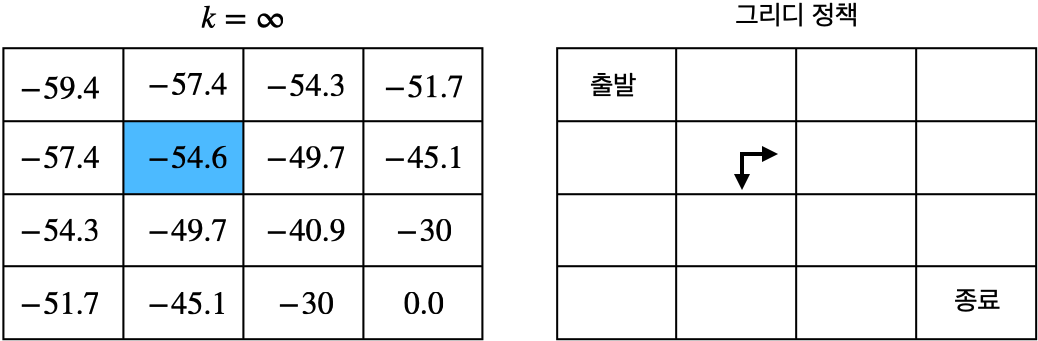
- $s_5$ 상태의 가치는 $-54.6$
◦ 북쪽 또는 서쪽으로 이동하면 $-57.4$로 가치가 작아짐
◦ 동쪽 또는 남쪽으로 이동하면 $-49.7$로 가치가 커짐
◦ 새로운 정책 $\pi'$을 생각할 수 있음
◦ $\pi'(a_{\text{동}} | s_5) = 1.0$ 또는 $\pi'(a_{\text{남}} | s_5) = 1.0$ - 그리디 정책(greedy policy): 먼 미래를 생각하지 않고 다음 칸의 가치가 가장 큰 것을 선택하는 것
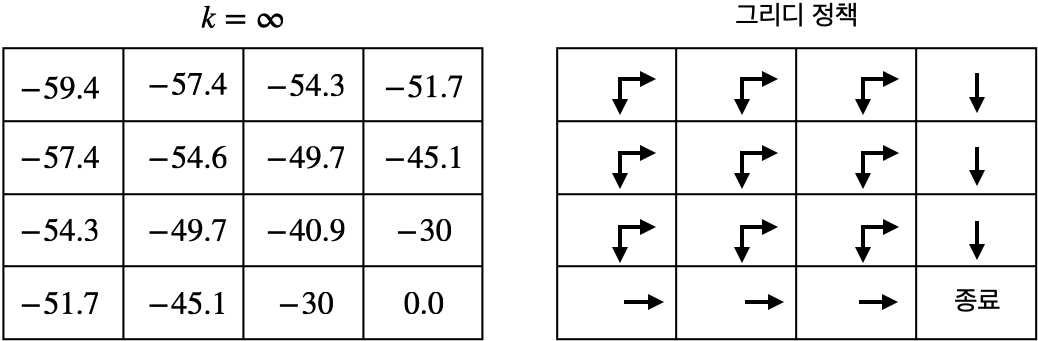
- 위 그림은 모든 상태에서 그리디 정책을 표시한 결과
- 랜덤 정책 $\pi$에 비해서 그리디 정책 $\pi'$가 개선됨. 이것이 정책 이터레이션(policy iteration)의 핵심
◈ 평가와 개선의 반복
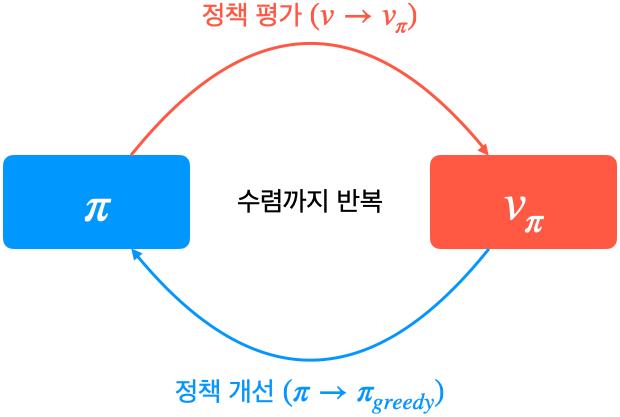
- 정책 이터레이션은 정책 평가(policy evaluation)와 정책 개선(policy improvement) 두 단계로 구성됨
- 정책 평가: 고정된 정채 $\pi$에 대해서 각 상태의 가치를 구함 (반복적 정책 평가)
- 정책 개선: 정책 평가의 결과에 따라 새로운 정책 $\pi'$ 생성 (그리디 정책 생성)
- 반복적으로 정책 평가와 정책 개선을 진행하면 정책과 가치가 변하지 않는 단계에 도달
최적 정책(optimal policy)과 최적 가치(optimal value) 임
◈ 과연 정책은 개선되는가?
- 아래와 같은 두 가지 정책을 가정
◦ $\pi$: 모든 상태에서 랜덤 정책
◦ $\pi_{greedy}$: $s_5$에서만 그리디 정책으로 움직이고 나머지 상태는 모두 랜덤 정책 - $s_5$에서는 $\pi_{greedy}$가 좋고 나머지 상태에서는 두 정책이 동일하기 때문에 $\pi_{greedy}$가 $\pi$ 보다 좋은 정책임
- 그리디 정책을 나머지 모든 상태에 적용해도 $\pi_{greedy}$가 $\pi$ 보다 좋은 정책임
◈ 정책 평가 부분을 간소화하기
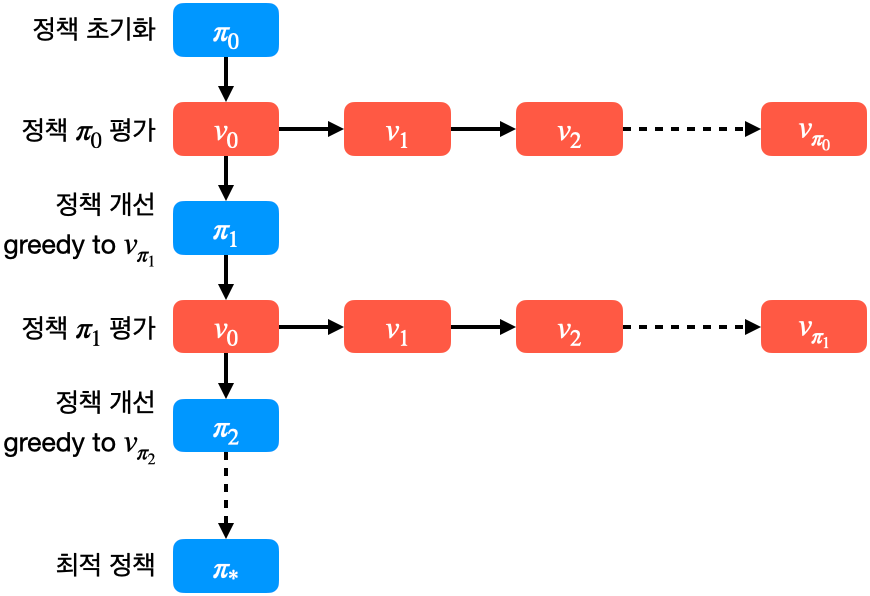
- 정책 이터레이션은 정책 평가와 정책 개선을 반복해서 수행.
- 정책 개선보다는 정책 평가에서 많은 연산을 수행
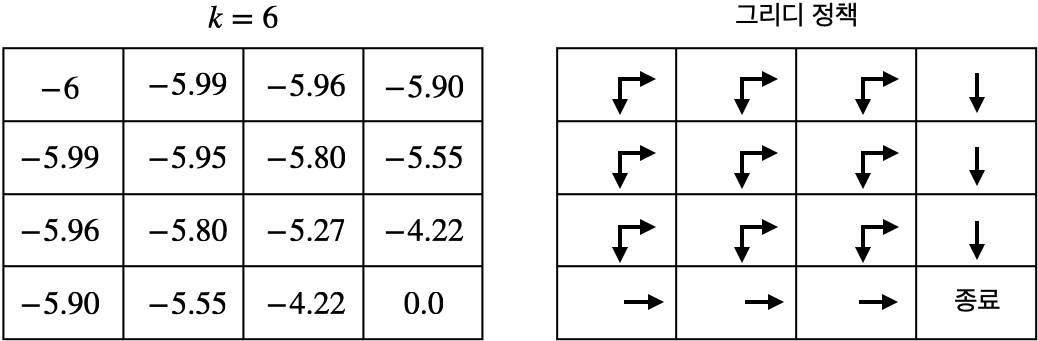
- 정책 평가를 6단계만 진행하고 일찍 멈춰(early stopping)도 최적의 정책에 도달 가능
- 최적의 정책을 찾는 것이 목적이지 정확한 가치 평가를 하는 것이 목적이 아님
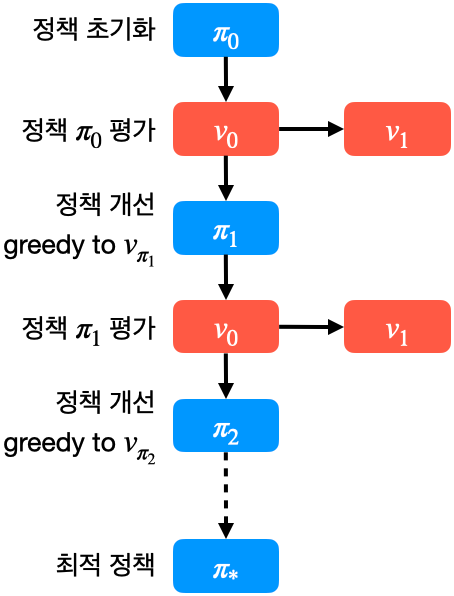
- 위 그림은 정책 평가를 1단계만 수행하고 정책 개선을 수행하는 경우의 정책 이터레이션
- 빠르게 정책 평가와 정책 개선이 가능하고, 빠르게 최적 정책을 찾을 수 있음
4.3 최고의 정책 찾기 - 밸류 이터레이션
- 밸류 이터레이션(value iteration): 최적 정책이 만들어낸 최적 밸류를 찾는 것
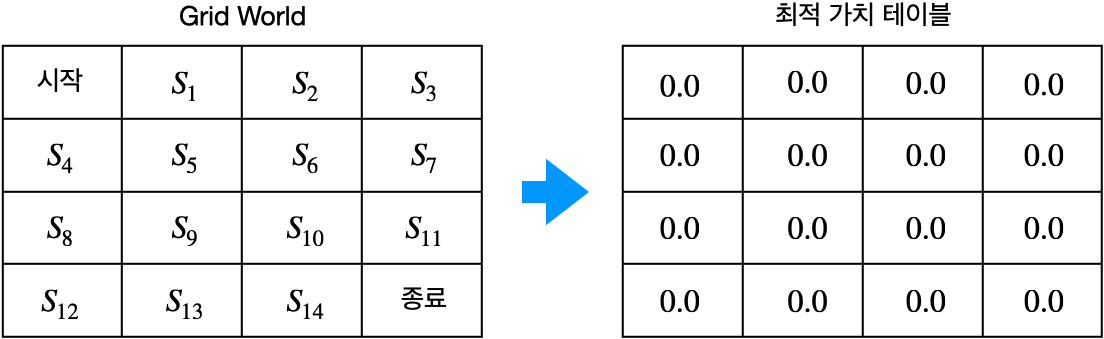
- 위 그림은 최적 밸류를 알 수 없으니 일단 0으로 테이블 초기화
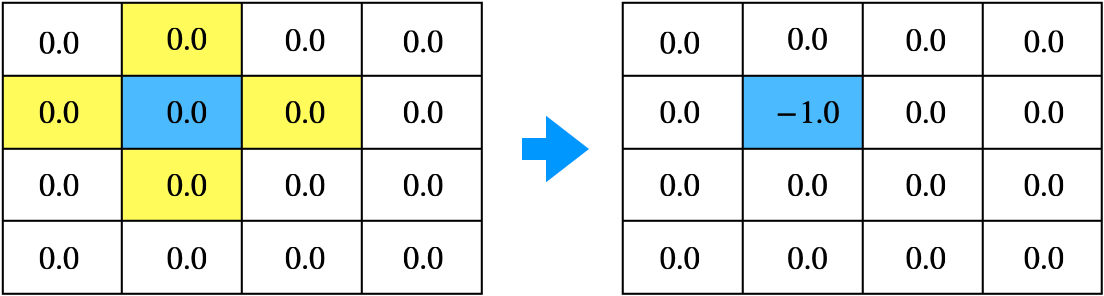
- 위 그림은 $s_5$의 최적 벨류를 벨만 최적 방정식을 이용해서 업데이트한 결과
$$\begin{equation}
\begin{split}
v_{*}(s) &= \underset{a}{\mathrm{max}} \left [ r_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_{*}(s') \right ] \\
&= \mathrm{max}(-1 + 1.0 * 0, -1 + 1.0 * 0, -1 + 1.0 * 0, -1 + 1.0 * 0,) \\
&= -1.0
\end{split}
\end{equation}$$
- 위 수식은 동, 서, 남, 북 네 가지 액션애 대한 중 최댓값을 사용
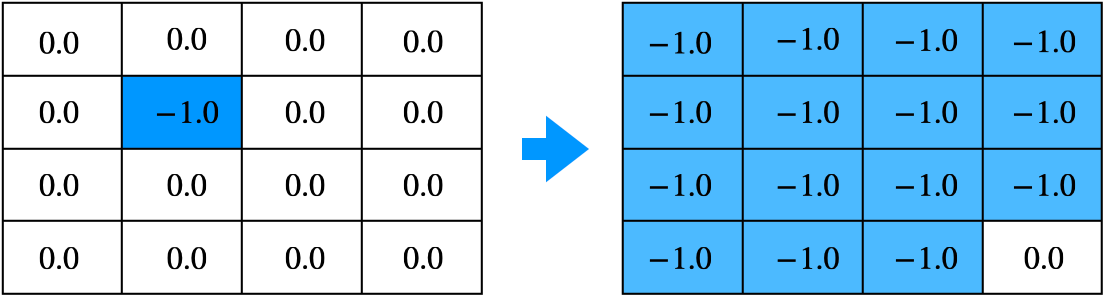
- 위 그림은 모든 상태 $s$에 대해서 벨만 최적 방정식을 이용해서 업데이트한 결과
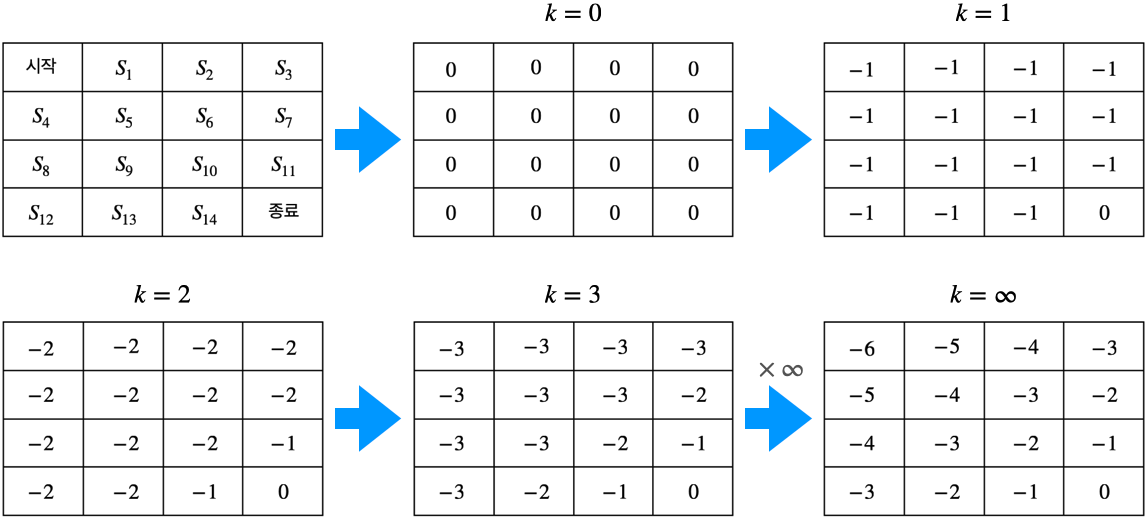
- 위 그림은 반복해서 벨만 최적 방정식을 이용해서 업데이트한 결과
- 최적 벨류를 알면 최적 정책을 얻을 수 있음. (최적 벨류에 대한 그리디 정책)
소스코드
아래 두 챕터의 내용을 직접 구현해 봤습니다.
- 4.1 밸류 평가하기 - 반복적 정책 평가
- 4.3 최고의 정책 찾기 - 벨류 이터레이션
https://github.com/with-rl/reinforcement-learning-from-basic/blob/main/ch_04.ipynb
'강화 학습 > 바닥부터 배우는 강화 학습' 카테고리의 다른 글
| 바닥부터 배우는 강화 학습 | 06. MDP를 모를 때 최고의 정책 찾기 (0) | 2023.01.05 |
|---|---|
| 바닥부터 배우는 강화 학습 | 05. MDP를 모를 때 밸류 평가하기 (0) | 2022.11.29 |
| 바닥부터 배우는 강화 학습 | 03. 벨만 방정식 (0) | 2022.11.04 |
| 바닥부터 배우는 강화 학습 | 02. 마르코프 결정 프로세스 (0) | 2022.11.04 |
| 바닥부터 배우는 강화 학습 | 01. 강화 학습이란 (2) | 2022.11.04 |