바닥부터 배우는 강화 학습 | 02. 마르코프 결정 프로세스

'바닥부터 배우는 강화 학습' 2장에는 중요한 기본 개념들을 설명하고 있습니다. 예전에 혼란스러웠던 내용인데 명쾌하게 잘 설명이 돼있습니다. 아래 내용은 공부하면서 핵심 내용을 정리한 것입니다.

참고자료

• 도서: 바닥부터 배우는 강화 학습 / 2장 마르코프 결정 프로세스
• 동영상: https://www.youtube.com/watch?v=NMesGSXr8H4

2.1 마르코프 프로세스 (Markov Process)

◈ 아이가 잠이 드는 마르코프 프로세스

• 위 그림의 예는 상태의 종류는 총 5가지, 매 1분마다 다음 상태로 상태 전이(state transition)
  ◦ $s_0$: 누워있는 상태. 시작 상태
  ◦ $s_1$: 일어나서 노는 상태
  ◦ $s_2$: 눈을 감은 상태
  ◦ $s_3$: 서서히 잠이 오는 상태
  ◦ $s_4$: 잠든 상태. 종료 상태(terminal state)
• Markov Process: $MP \equiv (S, P)$
  ◦ 상태 집합 $S = \{s_0, s_1, s_2, s_3, s_4\}$
      가능한 상태들을 모두 모아놓은 집합
  ◦ 전이 확률 행렬 $P_{ss'}=\mathbb {P}[S_{t+1}=s'|S_t=s]$
      상태 $s$에서 다음 상태 $s'$에 도착할 확률

◈ 마르코프 성질

• 마르코프 성질(Markov property): 미래는 오로지 현재에 의해 결정된다.
  $\mathbb {P}[s_{t+1}|s_t] = \mathbb {P}[s_{t+1}|s_1, s_2,..., s_t]$
• 다음 상태 $s_{t+1}$을 계산하려면 현재 상태 $s_t$만 주어지면 충분, 이전 상태들($s_1, s_2, ..., s_t$)은 영향을 주지 못함
• 미래는 오직 현재에 의해 결정되는 것

◈ 마르코프 한 상태

• 체스 게임의 경우 과거 이력이 아닌 현재 체스 판 상태를 보고 최선의 수를 둬야 함, 마르코프 한 상태
• 특정 시점의 체스판 사진만 보고도 다음에 어디에 둘지 결정 가능

◈ 마르코프 하지 않은 상태

• 운전의 경우는 특정 시점의 사진만으로는 다음 행동을 결정할 수 없음, 마르코프 하지 않은 상태
• 운전의 경우 최근 10초 동안의 사진 10장을 묶어서 상태로 제공한다면 마르코프 한 상태
• 비디오 게임을 플레이하는 인공지능을 학습시킬 때 $s_t, s_{t-1}, s_{t-2}, s_{t-2}$ 등 과거 이미지를 함께 상태로 제공, 마르코프 한 상태

2.2 마르코프 리워드 프로세스 (Markov Reward Processes)

마르코프 프로세스에 보상의 개념이 추가되면 마르코프 리워드 프로세스(Markov Reward Process)

◈ 아이가 잠이 드는 MRP

• Markov Reward Process: $MRP \equiv (S, P, R, \gamma)$
  ◦ 상태의 집합 $S$:
      마르코프 프로세스의 $S$와 같고 상태의 집합
  ◦ 전이 확률 행렬 $P$:
      마르코프 프로세스의 $P$와 같고 상태 $s$에서 $s'$으로 갈 확률의 행령
  ◦ 보상 함수 $R$:
      어떤 상태 $s$에 도착했을 때 받게 되는 보상
      $R=\mathbb {E}[R_t|S_t=s]$
  ◦ 감쇠 인자 $\gamma$: 0에서 1 사이의 숫자
      미래에 얻을 보상에 비해 당장 얻는 보상을 얼마나 더 중요하게 여길 것인지를 나타내는 파라미터

◈ 감쇠된 보상의 합, 리턴

• 에피소드(episode): $s_0$에서 $s_T$까지 가는 여정
  $s_0, R_0, s_1, R_1, s_2, R_2,..., s_T, R_T$
• 리턴(return): $t$시점부터 미래에 받을 감쇠된 보상의 합
  $G_t=R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} +...$
• 엄밀히 말하면 강화 학습은 보상이 아니라 리턴을 최대화하도록 학습

◈ $\gamma$는 왜 필요할까?

• $\gamma = 0$: 미래의 보상은 모두 0으로 현재의 보상만 생각하는 탐욕적(greedy)인 보상
• $0 < \gamma < 1$:여러 번 곱하면 0에 가까워짐, 현재의 보상이 100 스텝 후 받는 보상보다 훨씬 더 큰 값이 됨
• $\gamma = 1$: 현재의 보상과 미래의 보상이 동등, 장기적은 시야를 갖는 보상

 

수학적 편리성

• $\gamma$를 1보다 작게 해 줌으로써 리턴 $G_t$가 무한의 값을 가지는 것을 방지

 

사람의 선호 반영

• 5년 후에 받는 100만 원 보다는 현재 받는 100만 원을 선호함

 

미래에 대한 불확실성 반영

• 5년 후에 받을 100만 원에 대한 미래의 가치의 불확실성을 반영

◈ MRP에서 각 상태의 밸류 평가하기

• 현재 상태에서 미래에 받을 보상을 기준으로 평가
• 현재 상태 $s_t$의 가치를 평가하기 위해서 현재 상태 $s_t$에서 시작하여 리턴 $G_t$의 기댓값(expectation)을 측정

◈ 에피소드의 샘플링

• 에피소드: 시작 상태 $s_0$에서 출발하여 종료 상태 $s_t$까지 가능 한의 여정
• 샘플링 (sampling): 매번 에피소드는 다를 수 있으며 각각의 과정이 샘플링, 각 샘플링마다 리턴이 다를 수 있음
• 많은 경우 실제 확률 분포를 알기 어려우므로 샘플링을 통해 어떤 값을 유추하는 방법을 사용

◈ 상태 가치 함수 (State Value Function)

• 상태 가치 함수: $v(s) = \mathbb {E}[G_t|S_t=s]$

2.3 마르코프 결정 프로세스(Markov Decision Process)

마르코프 결정 프로세스(Markov Decision Process)는 순차적 의사 결정의 핵심인 의사결정(decision)에 관한 부분을 포함

◈ MDP의 정의

• Markov Decision Process: $MDP \equiv (S, A, P, R, \gamma)$
  ◦ 상태의 집합 $S$:
      가능한 상태의 집합으로 MP, MRP에서의 $S$와 같음
  ◦ 액션의 집합 $A$:
      에이전트가 취할 수 있는 액션들을 모아 놓은 것
      $A=\{ \text {앞으로 움직이기}, \text {뒤로 움직이기}, \text {흙을 채집하기} \}$
  ◦ 전이 확률 행렬 $P$:
      MP, MRP에서는 "현재 상태가 $s$일 때 다음 상태가 $s'$이 될 확률": $P_{ss'}$
      MDP에서는 "현재 상태가 $s$일 때 에이전트가 액션 a를 선택했을 때 다음 상태가 $s'$이 될 확률"
      $P_{ss'}^{a} = \mathbb {P} [S_{t+1}=s'|S_t=s, A_t=a]$
  ◦ 보상 함수 $R$:
      상태 $s$에서 액션 $a$를 선택하면 받는 보상 함수
      $R_s^a = \mathbb {E} [R_{t+1} | S_t=s, A_t=a]$
  ◦ 감쇠 인자 $\gamma$:
      MRP에서의 감쇠 인자 $gamma$와 정확히 같음

◈ 아이 재우기 MDP

• 위 그림의 전이 확률: $P_{s_2, s_0}^{a_1} = 0.3, P_{s_2, s_1}^{a_1} = 0.7$, 나머지는 모두 전이 확률이 1 (생략)

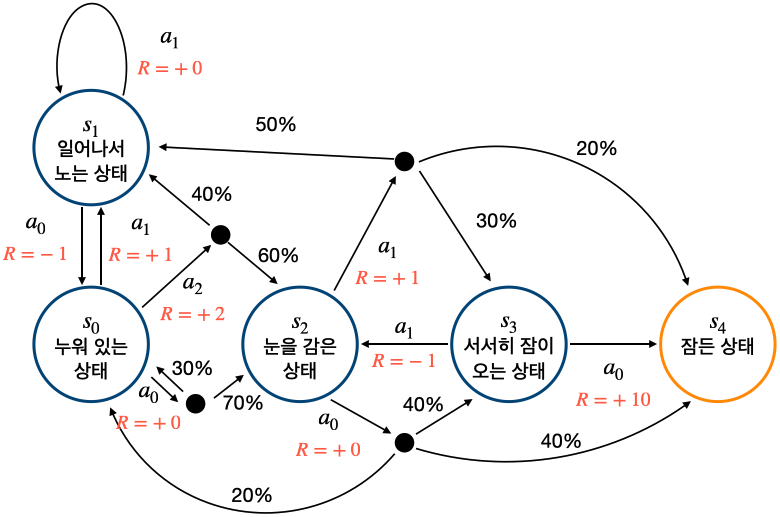
• 위 그림은 액션이 1개 늘어나서 복잡해진 MDP

◈ 정책 함수와 2가지 가치 함수

정책 함수

• 정책 함수(policy function)는 각 상태에서 어떤 액션을 선택할지 정해주는 함수
• $\pi(a|s) = \mathbb {P}[A_t=a|S_t=s]$
• 정책 함수는 에이전트 안에 존재
• 더 큰 보상을 얻기 위해 계속해서 정책을 교정해 나가는 것이 강화 학습

 

상태 가치 함수

• 상태 가치 함수(state value function): 에이전트의 정책 $pi$에 따라서 리턴 $G$이 달라짐

$$\begin {matrix}
v_{\pi}(s) &=& \mathbb {E_{\pi}} [r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} +... | S_t = s] \\
       &=& \mathbb {E_{\pi}}[G_t|S_t = s]
\end {matrix}$$

 

액션 가치 함수

• 액션 가치 함수(state-action value function): 각 상태에서 액션에 대한 가치 평가

$$q_{\pi}(s, a) = \mathbb {E}[G_t|S_t = s, A_t = a]$$

• 상태 가치 함수 $v_{\pi}(s)$는 상태 $s$에서 정책 $\pi$가 액션을 선택
• 액션 가치 함수 $q_{\pi}(s, a)$는 상태 $s$에서 강제로 액션을 선택

2.4 Prediction과 Control

• Prediction: 정책 $\pi$가 주어졌을 때 각 상태의 밸류를 평가하는 문제
• Control: 최적 정책 $\pi^{*}$를 찾는 문제, 리턴의 기댓값이 가장 큰 정책 $\pi$

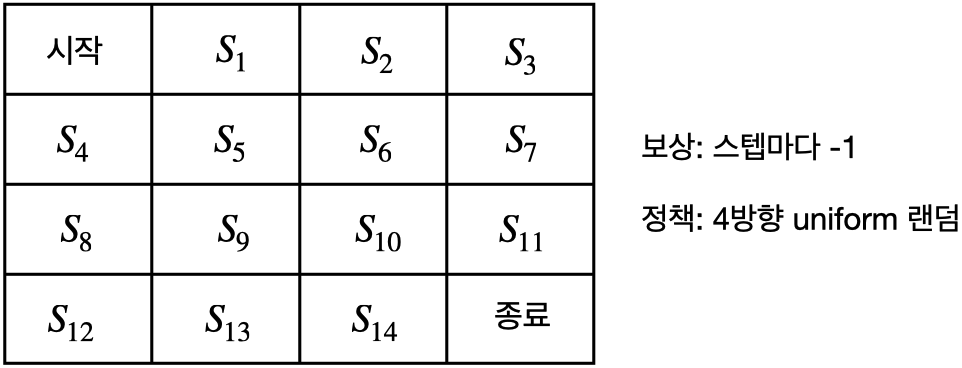
• 위 그림은 모든 상태 $s$에서 동, 서, 남, 북 액션을 선택할 확률이 25%인 경우
• 다양한 에피소드(Episode)가 있을 수 있고 각각 리턴이 다름 (아래 예는 $s_11$에서 시작한 경우의 에피소드)
  • $s_{11} \to \text{종료}, \;\;\;\;\text{리턴} = -1$
  • $s_{11} \to s_{10} \to s_{14} \to \text{종료}, \;\;\;\;\text{리턴} = -3$
  • $s_{11} \to s_{7} \to s_{6} \to s_{10} \to s_{11} \to \text{종료}, \;\;\;\;\text{리턴} = -5$

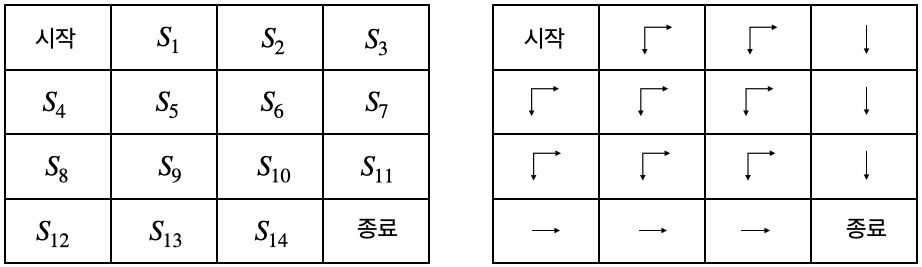
• 위 그림은 최적 정책 $\pi^*$
• 최적 가치 함수(optimal value function): 최적 정책 $\pi^*$를 따를 때의 가치 함수 $v^*$
• $\pi^*$과 $v^*$을 찾으면 "이 MDP는 풀렸다"라고 말할 수 있음