'바닥부터 배우는 강화 학습' 5장에는 MDP를 모르고 있는 경우 밸류를 평가하는 방법에 대해서 설명하고 있습니다. 아래 내용은 공부하면서 핵심 내용을 정리한 것입니다.
참고자료
- 도서: 바닥부터 배우는 강화 학습 / 5장 MDP를 모를 때 밸류 평가하기
- 동영상: https://www.youtube.com/watch?v=47FyZtBRglI&list=PLpRS2w0xWHTcTZyyX8LMmtbcMXpd3s4TU&index=4
모델 프리
- 보상 함수 $r_s^a$와 전이 확률 $P_{ss'}^a$를 모르는 상황
- '모델을 모른다', 'MDP를 모른다', '모델 프리다'는 같은 의미
5.1 몬테카를로 학습
- 동전의 앞면 뒷면이 나올 확률을 모르더라도 동전을 여러 번 던져보면 확률을 가늠할 수 있음
- 동전을 여러 번 던져볼수록 더 정확한 확률을 가늠할 수 있음
- 몬테카를로: 무언가 직접 측정하기 어려운 통계량이 있을 때 여러 번 샘플링하여 그 값을 가늠하는 기법
예) MCTS(Monte Carlo Tree Search), MCMC(Markov Chain Monte Carlo) - 가치 함수 $v_{\pi}(s_t)=\mathbb{E}(G_t)$를 계산할 때 실제 MDP를 모르더라도 상태 $s_t$에서 여러 번 리턴을 여러 번 구한 후 평균을 구해서 계산 가능
- 더 많은 에피소드를 진행할수록 대수의 법칙(Law of large numbers)에 의해 각 상태의 밸류 예측치는 점점 정확해짐
◈ 몬테카를로 학습 알고리즘
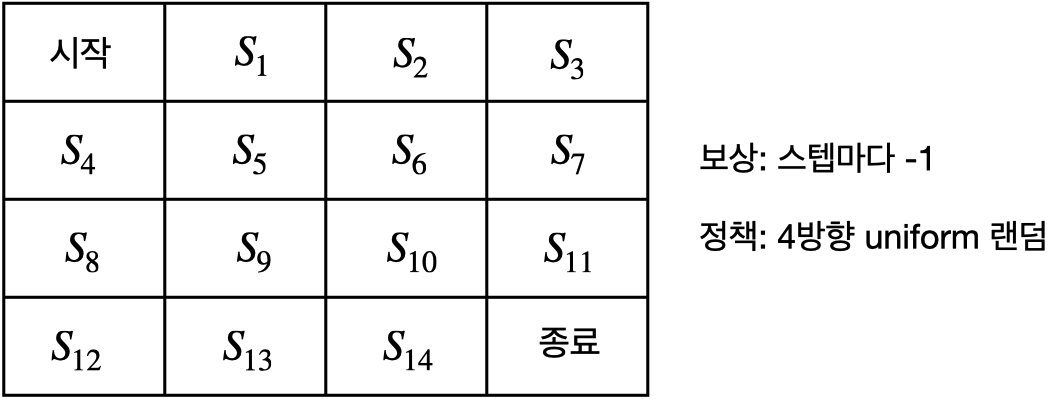
- 그리드 월드에서 보상 함수 $r_s^a$와 전이 확률 $P_{ss'}^a$를 모르는 상황
- 계산을 통해서 평가하는 플래닝(planning)이 아닌 실제 경험을 통한 학습
1. 테이블 초기화
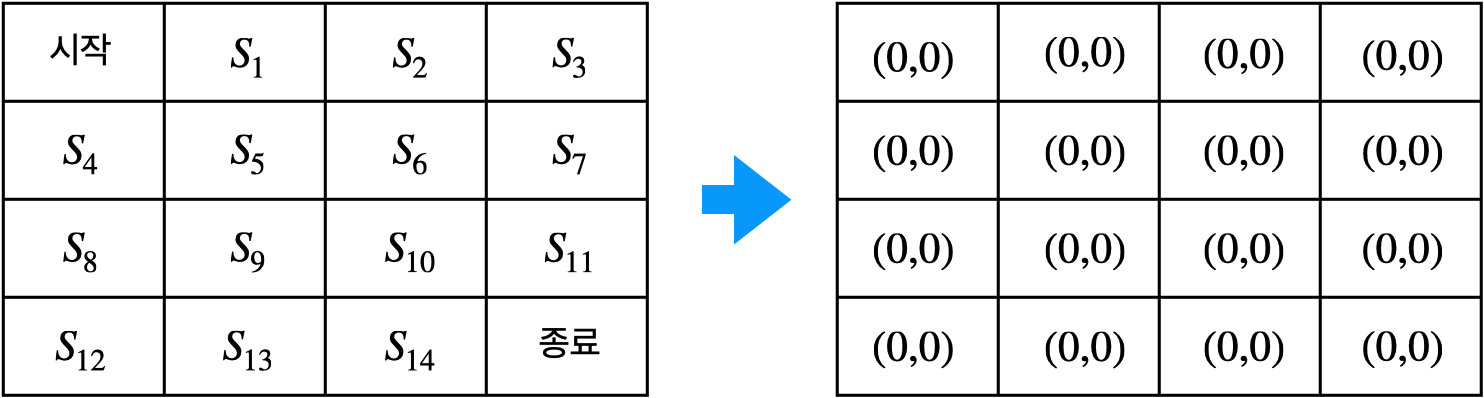
- 각 상태별로 $N(s)$와 $V(s)$ 2개의 값을 0으로 초기화
◦ $N(s)$: 상태 $s$를 총 몇 번 방문했는지 횟수를 기록
◦ $V(s)$: 상태 $s$에서 경험했던 리턴의 총합을 기록
2. 경험 쌓기
- 에이전트가 시작$(s_0)$ 에서 시작해서 종료$(s_T)$에 도달하기까지의 에피소드를 실행
$s_0, a_0, r_0, s_1, a_1, r_1, s_2, a_2, r_2, ..., s_{T-1}, a_{T-1}, r_{T-1}, s_T$ - 에피소드에 대한 리턴을 계산할 수 있음
$$\begin{equation}
\begin{split}
G_0 = r_0 + \gamma r_1 + \gamma^2 r_2 + \gamma^3 r_3 + ... + \gamma^{T-1} r_{T-1} \\
G_1 = r_1 + \gamma r_2 + \gamma^2 r_3 + ... + \gamma^{T-2} r_{T-1} \\
... \\
G_{T-1} = r_{T-1} \\
G_T = 0 \\
\end{split}
\end{equation}$$
3. 테이블 업데이트
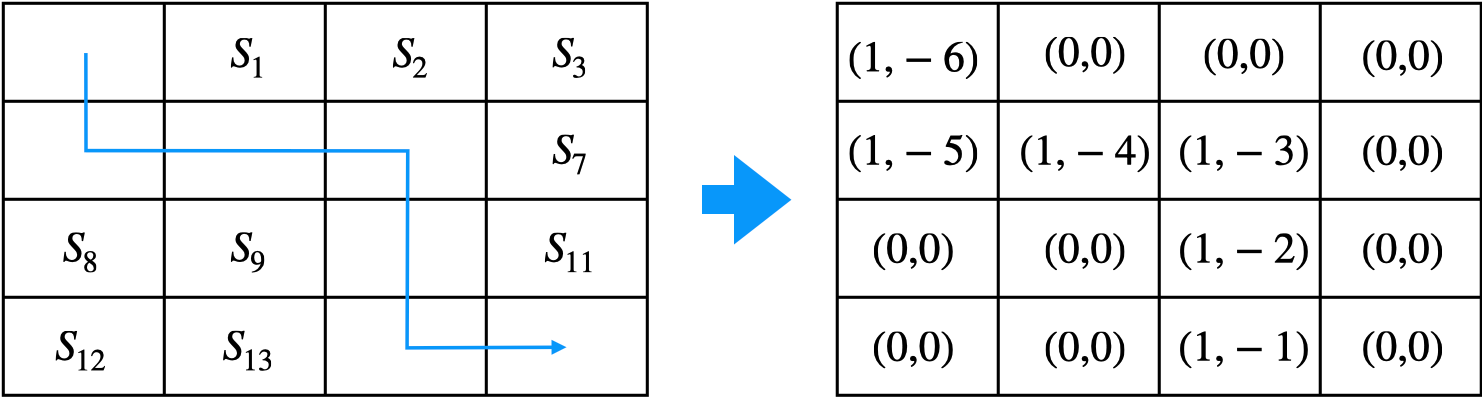
- 다음과 같은 에피소드를 실행하였다고 가정하면
$s_0 \to s_4 \to s_5 \to s_6 \to s_{10} \to s_{14} \to s_{T}$ - 방문했던 모든 상태에 대해서 $N(s)$와 $V(s)$값을 업데이트
◦ $N(s_t) \gets N(s_t) + 1$
◦ $V(s_t) \gets V(s_t) + G_t$
4. 밸류 계산
- 많은 횟수의 에피소드를 경험 후 충분히 경험이 쌓이면 리턴의 평균을 밸류의 근사치로 사용
$$v_{\pi}(s_t) \cong {V(s_t) \over N(s_t)}$$
- 이와 같이 많은 에피소드를 통해 밸류를 추정하는 방식이 몬테카를로 방법론
◈ 조금씩 업데이트하는 버전

- 에피소드가 1개 끝날 때마다 테이블의 값을 조금씩 업데이트
- $\alpha$는 얼마큼 업데이트할지 크기를 결정해주는 파라미터
- $N(s_t)$에 값을 따로 저장해 둘 필요 없이 에피소드가 끝날 때마다 테이블의 값을 업데이트
- 아래와 같이 표현도 가능함
$$V(s_t) \gets V(s_t) + \alpha * (G_t - V(s_t))$$
◈ 몬테카를로 학습 구현
이 부분은 구현에 대한 코드가 설명되어 있습니다.
5.2 Temporal Difference 학습
- MC(몬테카를로)의 한 가지 단점은 업데이트를 하려면 반드시 에피소드가 끝난 후에 리턴을 계산해야 함.
적용할 수 있는 환경이 제한 적 - Temporal Difference 학습 방법론: 종료하지 않는 MDP(non-terminating MDP)에서 학습 가능한 방법
◦ "에피소드가 끝나기 전에 업데이트할 수는 없을까?"
◦ "추측을 추측으로 업데이트 하자", "미래의 추측으로 과거의 추측을 업데이트"
◈ 이론적 배경
- 벨만 기대 방정식 0단계 수식
$$v_{\pi}(s_t) = \mathbb{E}_{\pi}[r_{t+1} + \gamma v_{\pi}(s_{t+1})]$$
- $r_{t+1} + \gamma v_{\pi} (s_{t+1})$을 여러 번 뽑아서 평균을 내면 그 평균이 $v_{\pi}(s_t)에 수렴$
- TD 타깃(TD target): $r_{t+1} + \gamma v_{\pi} (s_{t+1})$
◈ Temporal Difference 학습 알고리즘
- TD도 MC와 마찬가지로 테이블 값을 0으로 초기화
- TD와 MC의 차이는 업데이트 수식과 업데이트 시점이 다름
- 아래의 에피소드를 가정
$s_0 \to s_1 \to s_2 \to s_3 \to s_7 \to s_6 \to s_{10} \to s_{11} \to s_T$ - TD는 각각의 상태 전이가 일어나자마자 바로 테이블의 값을 업데이트
◦ MC: $V(s_t) \gets V(s_t) + \alpha(G_t - V(s_t))$
◦ TD: $V(s_t) \gets V(s_t) + \alpha (r_{t+1} + \gamma V(s_{t+1}) - V(s_t))$ - 위 수식은 MC의 $G_t$를 $r_{t+1} + \gamma V(s_{t+1})$로 변경한 것
- 모든 상태에서 보상은 -1, $\alpha = 0.01$, $\gamma = 1.0$인 경우 아래와 같이 계산 가능
$$\begin{equation}
\begin{split}
V(s_0) &\gets V(s_0) + 0.01 * (-1 + V(s_1) - V(s_0)) \\
V(s_1) &\gets V(s_1) + 0.01 * (-1 + V(s_2) - V(s_1)) \\
... \\
V(s_{11}) &\gets V(s_{11}) + 0.01 * (-1 + V(s_{15}) - V(s_{11})) \\
\end{split}
\end{equation}$$
- 테이블의 값이 수렴할 때까지 진행
◈ Temporal Difference 학습 구현
이 부분은 구현에 대한 코드가 설명되어 있습니다.
5.3 몬테카를로 vs TD
- MC, TD의 장점을 여러 측면에서 비교
◈ 학습 시점
- Episodic MDP: MDP의 상태들 중에 종료 상태(terminating state)라는 것이 있는 경우
◦ 바둑, 스타크래프트 등 종료 조건이 명확한 경우
◦ MC, TD 모두 적용 가능 - Non-Episodic MDP: 종료 상태 없이 하나의 에피소드가 무한히 이어지는 MDP
◦ 주식 시장에서의 포트폴리오 분배처럼 명확한 종료 조건이 없거나, 하나의 에피소드가 너무 길어지는 경우
◦ TD만 적용 가능
◈ 편향성(Bias)
- MC: $v_{\pi}(s_t) = \mathbb{E}[(G_t)]$. (from 가치 함수의 정의)
◦ 여러 개의 샘플에 대한 평균을 구하는 방식으로 편향되어 있지 않는(unbiased) 안전한 방법론 - TD: $v_{\pi}(s_t) = \mathbb{E}[(r_{t+1} + \gamma v_{\pi}(s_{t+1}))]$ (from 벨만 기대 방정식)
◦ 실제 계산에서 사용하는 수식은 $v_{\pi}(s_t) = \mathbb{E}[(r_{t+1} + \gamma V(s_{t+1}))]$
◦ $v_{\pi}$: 정책 $\pi$의 실제 가치로 알 수 없는 값
◦ $V$: 현재 업데이트하고 있는 테이블에 쓰여있는 값
◦ $v_{\pi}(s_{t+1}) \ne V(s_{t+1})$
◦ 실제 타깃 $r_{t+1} + \gamma v_{\pi}(s_{t+1})$은 불편 추정량(unbiased estimate)
◦ 사용하는 타깃 $r_{t+1} + \gamma V(s_{t+1})$은 편향(biased) 되어 있음 - 편향성의 측면에서는 MC가 우세
◈ 분산(Variance)
- MC는 에피소드가 끝나야 하기 때문에 리턴이 -6 또는 -2000 등 다양한 값을 가질 수 있음. 분산(variance)이 큼
- TD는 한 샘플만 보고 업데이트하기 때문에 분산이 작음
- 분산의 측면에서는 TD가 우세
◈ 종합
- 최근 강화 학습 알고리즘은 TD가 우세
5.4 몬테카를로와 TD의 중간
◈ n스텝 TD
- TD에서 여러 스텝을 진행하고 난 뒤 추측 치를 이용
$$\begin{equation}
\begin{split}
N = 1: &r_{t+1} + \gamma V(s_{t+1}) \\
N = 2: &r_{t+1} + \gamma r_{t+2} + \gamma^2 V(s_{t+2}) \\
N = 3: &r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \gamma^3 V(s_{t+3}) \\
... \\
N = n: &r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+2} + ... + \gamma^n V(s_{t+n}) \\
\end{split}
\end{equation}$$
- 스텝을 무한으로 간다면 (종료 시점을 T로 가정)
$$N = \infty: r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+2} + ... + \gamma^{T-1} R_T$$
- 위 값은 리턴임. 즉 MC는 TD의 한 사례
- TD(0): N=1인 경우의 TD를 TD-zero라고 함
- N이 커질수록 bias는 줄어들고 variance는 커짐
- TD(0)와 MC 사이의 적당한 구간을 찾는 것은 어려운 문제
'강화 학습 > 바닥부터 배우는 강화 학습' 카테고리의 다른 글
| 바닥부터 배우는 강화 학습 | 07. Deep RL 첫 걸음 (0) | 2023.01.17 |
|---|---|
| 바닥부터 배우는 강화 학습 | 06. MDP를 모를 때 최고의 정책 찾기 (0) | 2023.01.05 |
| 바닥부터 배우는 강화 학습 | 04. MDP를 알 때의 플래닝 (0) | 2022.11.14 |
| 바닥부터 배우는 강화 학습 | 03. 벨만 방정식 (0) | 2022.11.04 |
| 바닥부터 배우는 강화 학습 | 02. 마르코프 결정 프로세스 (0) | 2022.11.04 |