'바닥부터 배우는 강화 학습' 6장에는 MDP를 모르고 있는 경우 최고의 정책을 찾는 방법에 대해서 설명하고 있습니다. 아래 내용은 공부하면서 핵심 내용을 정리한 것입니다.
참고자료
- 도서: 바닥부터 배우는 강화 학습 / 6장 MDP를 모를 때 최고의 정책 찾기
- 동영상: https://www.youtube.com/watch?v=2h-FD3e1YgQ&list=PLpRS2w0xWHTcTZyyX8LMmtbcMXpd3s4TU&index=5
6.1 몬테카를로 컨트롤
◈ 정책 이터레이션을 그대로 사용할 수 없는 이유
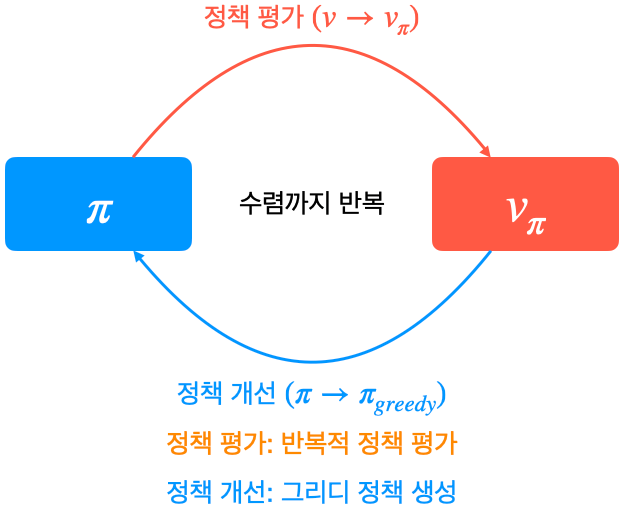
- 첫 번째: 반복적인 정책평가를 사용할 수 없음
모델 프리 상황에서는 보상함수 $r_s^a$와 전이확률 $P_{ss'}^a$을 모르기 때문에 아래 벨만 기대 방정식을 사용할 수 없음
$$v_{\pi}(s) = \sum_{a \in A} \pi(a|s) \left( r_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_{\pi}(s') \right)$$
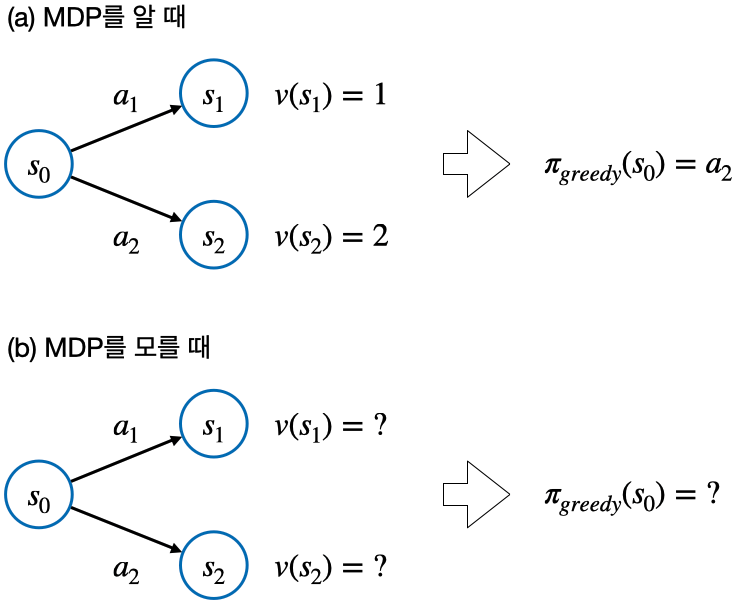
- 두 번째: 정책 개선 단계에서 그리디 정책을 만들 수 없음
각 상태의 밸류를 안다고 하더라도 전이확률 $P_{ss'}^a$을 모르기 때문에 액션을 취했을 때 어떤 상태에 도달할지 알 수 없음
◈ 해결 방법
1. 평가 자리에 MC
- 몬테카를로 방법론을 이용해서 각 상태의 밸류 $v(s)$를 구할 수 있음
2. V 대신 Q
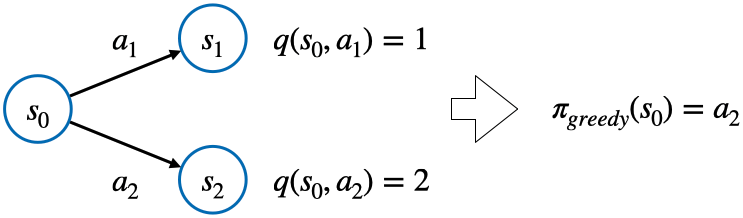
- 밸류 $v(s)$ 대신에 상태-액션 가치 함수 $q(s, a)$를 이용 (MDP를 몰라도 그리디 액션을 선택할 수 있음)
◦ MC를 이용하여 $q(s, a)$ 함수를 계산
◦ 평가된 $q(s, a)$를 이용하여 새로운 그리디 정책을 생성
◦ 위 두 과정을 반복 - 위 방법은 새로운 길을 탐색하지 못하므로 최적의 해를 찾지 못할 수 있음
3. greedy 대신 $\epsilon$ - greedy
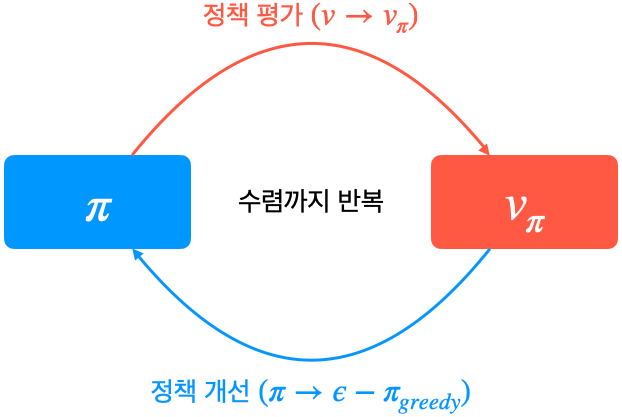
- $\epsilon$라는 작은 확률만큼 랜덤 하게 액션을 선택하고, 나머지 $1 - \epsilon$ 확률은 원래 그리디 액션을 선택
$$\pi(a|s)=
\begin{cases}
1 - \epsilon, & \mbox{if } a* = \underset{a}{\mathrm{argmax}} \; q(s, a) \\
\epsilon, & \text{otherwise}
\end{cases}$$
- decaying $\epsilon$ - greedy: 처음에는 $\epsilon$을 큰 값을 사용하고 이후 점점 줄여주는 학습방법
◈ 몬테카를로 컨트롤 구현
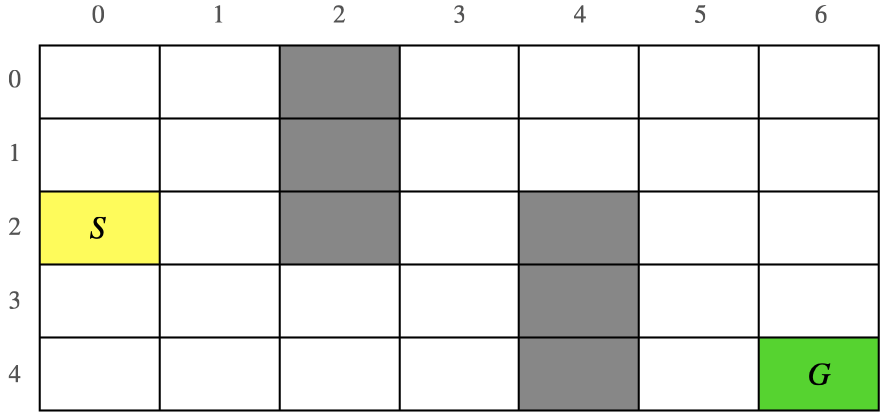
- 이 부분은 아래 문제를 해결하기 위한 구현에 대한 코드가 설명되어 있습니다.
◦ S에서 출발 해서 G에 도착하면 끝
◦ 회색 영역은 지나갈 수 없는 벽이 놓여 있는 곳
◦ 보상은 스텝마다 -1 (즉 최단 거리로 G에 도달하는 것이 목적)
6.2 TD 컨트롤 1 - SARSA
◈ MC 대신 TD
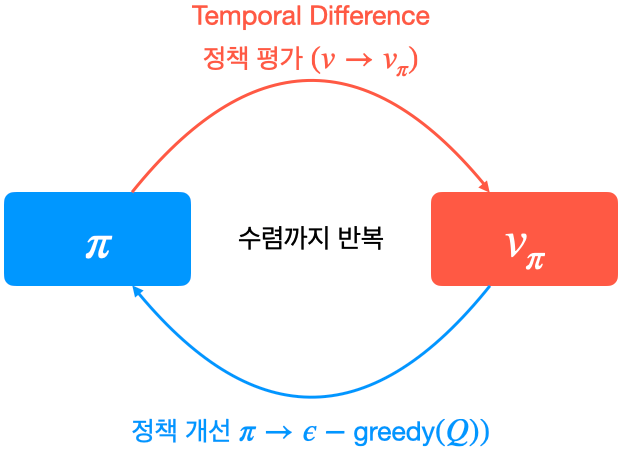
- MC 대신 TD를 사용
- SARSA: TD를 이용해 Q를 계산하는 접근 법
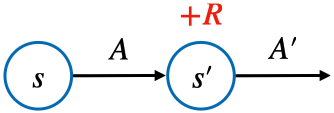
- TD를 이용한 V 학습 및 Q 학습의 수식
◦ TD로 V 학습: $V(S) \gets V(S) + \alpha (R + \gamma V(S') - V(S))$
◦ TD로 Q 학습 (SARSA): $Q(S, A) \gets Q(S, A) + \alpha (R + \gamma Q(S', A') - Q(S, A))$ - 벨만 기대 방정식 0단계
◦ TD로 V 학습: $v_{\pi}(s_t) = \mathbb{E} [r_{t+1} + \gamma v_{\pi}(s_{t+1})]$
◦ TD로 Q 학습 (SARSA): $q_{\pi}(s_t, a_t) = \mathbb{E} [r_{t+1} + \gamma q_{\pi}(s_{t+1}, a_{t+1})]$
◈ SARSA 구현
이 부분은 구현에 대한 코드가 설명되어 있습니다.
6.3 TD 컨트롤 2 - Q러닝
◈ Off-Policy와 On-Policy
- 타깃 정책 (target policy): 강화하고자 하는 목표가 되는 정책
- 행동 정책 (behaviro policy): 실제로 환경과 상호 작용하며 경험을 쌓고 있는 정책
- On-Policy: 타깃 정책과 행동 정책이 같은 경우 (직접 경험)
- Off-Policy: 타깃 정책과 행동 정책이 다른 경우 (간접 경험), 타깃 정책은 행동 정책의 좋은 점은 수용 좋지 않은 점은 수정
◈ Off-policy 학습의 장점
1 과거의 경험을 재사용할 수 있다
- on-policy 방법은 $\pi_t$ 에서 $\pi_{t+1}$을 학습하기 위해서는 항상 $\pi_t$을 따르는 새로운 경험이 필요
- off-policy 방법은 타깃 정책과 행동 정책이 달라도 되기 때문에 $\pi_t$ 에서 경험한 샘플들을 $\pi_{t+1}$ 및 $\pi_{t+n}$ 등 여러 정책에서 재사용 가능
2 사람의 데이터로부터 학습할 수 있다
- 프로 바둑 기사가 뒀던 기보를 $(s, a, r, s')$ 형식으로 만들어서 off-policy 학습이 가능
3 일대다, 다대일 학습이 가능하다
- 동시에 여러 개의 정책이 겪은 데이터를 모아서 1개의 정책을 업데이트할 수 있음
- 행동 정책과 타깃 정책이 달라도 되기 때문에 다양한 관점에서 학습이 자유로움
◈ Q러닝의 이론적 배경 - 벨만 최적 방정식
- 최적의 액션 밸류: $q_{*}(s, a) = \underset{\pi}{\mathrm{max}} \; q_{\pi}(s, a)$
- 최적의 행동: $\pi_{*} = \underset{a}{\mathrm{argmax}} \; q_{*}(s, a)$
- 벨만 최적 방정식 2단계: $q_{*}(s, a) = r_s^a+ \gamma \sum_{s' \in S} P_{ss'}^a \underset{a'}{\mathrm{max}} \; q_{*} (s', a')$
MDP를 모르기 때문에 위 수식을 그대로 이용할 수 없음 - 벨만 최적 방정식 0단계: $q_{*}(s, a) = \mathbb{E}_{s'} [r + \gamma \; \underset{a'}{\mathrm{max}} \; q_{*} (s', a')]$
위 수식은 TD 학습이 가능 - SARSA: $Q(S, A) \gets Q(S, A) + \alpha (R + \gamma Q(S', A') - Q(S, A))$
- Q러닝: $Q(S, A) \gets Q(S, A) + \alpha (R + \gamma \; \underset{A'}{\mathrm{max}} \; Q(S', A') - Q(S, A))$
| SARSA | Q러닝 | |
| 행동정책 (Behavior Policy) |
Q에 대해 $\epsilon$-Greedy |
Q에 대해 $\epsilon$-Greedy |
| 타깃 정책 (Target Policy) |
Q에 대해 $\epsilon$-Greedy |
Q에 대해 Greedy |
- SARSA의 경우는 행동 정책과 타깃 정책이 같지만 Q러닝의 경우 행동 정책과 타깃 정책이 다름
- SARSA: $q_{\pi}(s_t, a_t) = \mathbb{E}_{\pi} [r_{t+1} + \gamma q_{\pi}(s_{t+1}, a_{t+1})]$
- Q러닝: $q_{*}(s_t, a_t) = \mathbb{E}_{s'} [r + \gamma \; \; \underset{a'}{\mathrm{max}} \; q_{*}(s', a')]$
- $\mathbb{E}_{\pi}$는 정책 함수 $\pi$를 따라가는 경로에 대한 기댓값이 필요
- $\mathbb{E}_{s'}$는 정책 함수 $\pi$와 상관없음
◈ Q러닝 구현
이 부분은 구현에 대한 코드가 설명되어 있습니다.
'강화 학습 > 바닥부터 배우는 강화 학습' 카테고리의 다른 글
| 바닥부터 배우는 강화 학습 | 08. 가치 기반 에이전트 (0) | 2023.01.21 |
|---|---|
| 바닥부터 배우는 강화 학습 | 07. Deep RL 첫 걸음 (0) | 2023.01.17 |
| 바닥부터 배우는 강화 학습 | 05. MDP를 모를 때 밸류 평가하기 (0) | 2022.11.29 |
| 바닥부터 배우는 강화 학습 | 04. MDP를 알 때의 플래닝 (0) | 2022.11.14 |
| 바닥부터 배우는 강화 학습 | 03. 벨만 방정식 (0) | 2022.11.04 |