'바닥부터 배우는 강화 학습' 9장에는 정책 기반 에이전트를 학습하는 방법에 대해서 설명하고 있습니다. 아래 내용은 공부하면서 핵심 내용을 정리한 것입니다.
참고자료
- 도서: 바닥부터 배우는 강화 학습 / 9장 정책 기반 에이전트
9.1 Policy Gradient
- 가치 기반 에이전트가 액션을 선택하는 방식은 결정론적(deterministic): 모든 상태 $s$에 대해 각 상태에서 선택하는 액션이 변하지 않음
- 정책 기반 에이전트는 확률적 정책(stochastic policy): $\pi(s, a) = \mathbb{P}[a|s]$
- 정책 기반 에이전트는 가치 기반 에이전트에 비해 좀 더 유연한 정책을 가질 수 있음
- 액션 공간(action space)이 연속적(continuous)인 경우 (예, 0에서 1 사이의 모든 실수값이 액션으로 선택될 수 있는 상황)
◦ 가치 기반 에이전트는 모든 $a \in [0, 1]$에 대해서 Q(s, a)의 값을 최대로 하는 $a$를 찾아야 함
◦ 연속적 액션 공간에서는 $Q(s, a)$ 기반 에이전트가 작동하기 힘듦
◦ 정책 기반 에이전트는 $\pi(s)$가 주어져 있다면 바로 액션을 뽑을 수 있음
◦ 환경에 숨겨진 정보가 있거나 환경이 변하는 경우에도 더 유연하게 대처할 수 있음 - 이번 챕터에서 다룰 문제
◦ 모델 프리
◦ 커다란 문제여서 테이블에 담을 수 없음
◦ 정책 네트워크(policy network)를 강화하는 것이 목적
◈ 목적 함수 정하기
- 정책 네트워크: $\pi_{\theta}(s, a)$
- 정책 네트워크 파라미터: $\theta$
- 정책을 평가하는 함수: $J(\theta)$
- 그라디언트 어센트(gradient ascent): 정책을 평가하는 기준을 세워서 그 값을 증가시키도록 하는 방향으로 그라디언트를 업데이트
- $J(\theta)$는 보상의 합에 기댓값을 취한 것
◦ $J(\theta) = \mathbb{E}_{\pi_{\theta}} \left [ \sum_t r_t \right ]$ - 시작하는 상태가 $s_0$로 고정되어 있다면 $s_0$의 가치라고 볼 수 있음
◦ $J(\theta) = \mathbb{E}_{\pi_{\theta}} \left [ \sum_t r_t \right ] = v_{\pi_{\theta}}(s_0)$ - 시작하는 상태가 고정되어 있지 않고 시작 상태 $s$의 확률 분포 $d(s)$가 정의되어 있다면
◦ $J(\theta) = \sum_{s \in S} d(s) * v_{\pi_{\theta}}(s)$ - 그리디언트 기반으로 $J(\theta)$를 최대화
◦ $\theta' \gets \theta + \alpha * \nabla_{\theta} J(\theta)$
◈ 1-Step MDP
- 1-Setp MDP: 딱 한 스텝만 진행하고 바로 에피소드가 끝나는 MDP
$$\begin{equation}
\begin{split}
J(\theta) &= \sum_{s \in S} d(s) * v_{\pi_{\theta}}(s) \\
&= \sum_{s \in S} d(s) \sum_{a \in A} \pi_{\theta}(s, a) * R_{s, a} \\
\nabla_{\theta}J(\theta) &= \nabla_{\theta} \sum_{s \in S} d(s) \sum_{a \in A} \pi_{\theta}(s, a) * R_{s, a}
\end{split}
\end{equation}$$
- 모델-프리 상황에서는 $R_{s,a}$와 $P_{ss'}^a$를 알 수 없음
- $R_{s,a}$를 안다고 해도 상태 $s$가 많은 경우 계산 불가능
$$\begin{equation}
\begin{split}
\nabla_{\theta}J(\theta) &= \nabla_{\theta} \sum_{s \in S} d(s) \sum_{a \in A} \pi_{\theta}(s, a) * R_{s, a} \\
&= \sum_{s \in S} d(s) \sum_{a \in A} \nabla_{\theta} \pi_{\theta}(s, a) * R_{s, a} \\
&= \sum_{s \in S} d(s) \sum_{a \in A} {\pi_{\theta}(s, a) \over \pi_{\theta}(s, a)} \nabla_{\theta} \pi_{\theta}(s, a) * R_{s, a} \\
&= \sum_{s \in S} d(s) \sum_{a \in A} \pi_{\theta}(s, a) {\nabla_{\theta} \pi_{\theta}(s, a) \over \pi_{\theta}(s, a)} * R_{s, a} \\
&= \sum_{s \in S} d(s) \sum_{a \in A} \pi_{\theta}(s, a) \nabla_{\theta} \log \pi_{\theta}(s, a) * R_{s, a} \\
\end{split}
\end{equation}$$
- 위와 같이 식의 형태를 조금 바꾸면 "샘플 기반 방법론"으로 우변 값 계산 가능
$$\begin{equation}
\begin{split}
\nabla_{\theta}J(\theta) &= \sum_{s \in S} d(s) \sum_{a \in A} \pi_{\theta}(s, a) \nabla_{\theta} \log \pi_{\theta}(s, a) * R_{s, a} \\
&= \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * R_{s, a} \right ]
\end{split}
\end{equation}$$
- 위 수식과 같이 기댓값 연산자를 이용해 간단하게 식 변경 가능
- $\nabla_{\theta} \log \pi_{\theta}(s, a) * R_{s, a}$의 값을 여러 개 모아서 평균을 내면 그 값이 $\nabla_{\theta}J(\theta)$와 같음
◈ 일반적 MDP에서의 Policy Gradient
- 1step MDP: $\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * R_{s, a} \right ]$
- MDP : $\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * Q_{\pi_{\theta}} (s, a) \right ]$
- MDP에서는 한 스텝만 밟고 MDP가 종료되는 게 아니라 이후에 여러 스텝이 있기 때문에 이후에 받을 보상까지 포함
- 목적 함수에 대한 그라디언트를 $\pi_{\theta}(s, a)$가 경험한 데이터를 기반으로 계산할 수 있게 해주는 방법론이 policy gradient
9.2 REINFORCE 알고리즘
- REINFORCE 알고리즘은 policy gradient 알고리즘 중에서도 가장 기본적이고, 고전적이면서 간단한 알고리즘
◈ 이론적 배경
- Policy gradient theorem의 원래 수식에서 약간 변형
◦ $\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * G_t \right ]$ - $G_t$의 샘플을 여러 개 얻어 평균을 내면 $Q_{\pi_{\theta}}(s, a)$에 근사해짐
◦ $Q_{\pi_{\theta}}(s, a) = \mathbb{E} \left [ G_t | s_t = s, a_t = a \right ]$ - 기댓값 연산자 안에서 $Q_{\pi_{\theta}} (s, a)$를 $G_t$로 대체 가능
REINFORCE pseudo code
- $\pi_{\theta}(s, a)$의 파라미터 $\theta$를 랜덤으로 초기화
- 다음을 반복
◦ 에이전트의 상태를 초기화: $s \gets s_0$
◦ $\pi_{\theta}$를 이용하여 에피소드 끝까지 진행, $\{ s_0, a_0, r_0, s_1, a_1, r_1, ..., s_T, a_T, r_T\}$을 얻음
◦ $t=0 \backsim T$에 대해 다음을 반복
◦ $G_t \gets \sum_{i=t}^T r_i * \gamma^{i - t}$
◦ $\theta \gets \theta + \alpha * \nabla_{\theta} \log \pi_{\theta} (s_t, a_t) * G_t$
- $\nabla_{\theta} \log \pi_{\theta} (s, a) * G_t$에서 $G_t$를 무시하고 $\nabla_{\theta} \log \pi_{\theta} (s, a)$만 가지고 업데이트한다면 다음과 같은 형태
◦ $\theta \gets \theta + \alpha * \nabla_{\theta} \log \pi_{\theta} (s, a)$ - 위 수식의 의미는 $\log \pi_{\theta} (s, a)$를 증가시킨다는 의미이고 $\pi_{\theta} (s, a)$를 증가시키겠다는 의미와 같음
- $G_t$가 +1일 때와 -1일 때의 경우
◦ $G_t = 1$: $\theta \gets \theta + \alpha * \nabla_{\theta} \log \pi_{\theta} (s, a) * 1$
$\log \pi_{\theta} (s, a)$를 증가시키는 방향으로 업데이트
◦ $G_t = -1$: $\theta \gets \theta - \alpha * \nabla_{\theta} \log \pi_{\theta} (s, a) * 1$
$\log \pi_{\theta} (s, a)$를 감소시키는 방향으로 업데이트
◦ 좋은 액션의 확률은 증가시키도록 업데이터 안 좋은 액션은 그만하라고 억제함
- $G_t$가 +1일 때와 +100일 때의 경우
◦ $G_t = 1$: $\theta \gets \theta + \alpha * \nabla_{\theta} \log \pi_{\theta} (s, a) * 1$
$\log \pi_{\theta} (s, a)$를 1만큼 크기로 업데이트
◦ $G_t = 100$: $\theta \gets \theta + \alpha * \nabla_{\theta} \log \pi_{\theta} (s, a) * 100$
$\log \pi_{\theta} (s, a)$를 100만큼 크기로 업데이트
◦ $\pi_{\theta} (s, a)$는 확률이고 리턴이 더 좋았던 쪽의 액션이 더 많이 강화됨
- $\nabla_{\theta} \log \pi_{\theta} (s, a)$ 대신 $\nabla_{\theta} \pi_{\theta} (s, a)$를 사용하는 것은 불가
◦ $\nabla_{\theta}J(\theta) \ne \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \pi_{\theta}(s, a) * G_t \right ]$ 식이 성립하지 않음
◈ REINFORCE 구현
- 데이터가 주어졌을 때, 데이터를 이용해 계산하는 식
◦ $J(\theta) \approx G_t * \log \pi_{\theta}(s_t, a_t)$
◦ $\nabla_{\theta}J(\theta) \approx G_t * \nabla_{\theta} \log \pi_{\theta}(s_t, a_t)$ - 파이토치나 텐서플로우는 minimize 하는 방향으로 업데이트하기 때문에 $-$를 붙여서 식을 변형
◦ $J(\theta) \approx -G_t * \log \pi_{\theta}(s_t, a_t)$
◦ $\nabla_{\theta}J(\theta) \approx -G_t * \nabla_{\theta} \log \pi_{\theta}(s_t, a_t)$ - 이 부분은 구현에 대한 코드가 설명되어 있습니다.
9.3 액터-크리틱
- 정책 네트워크와 밸류 네트워크를 함께 학습하는 방법
◈ Q 액터-크리틱
- Policy gradient 수식
◦ $\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * Q_{\pi_{\theta}} (s, a) \right ]$ - 액터(actor): $\pi_{\theta}$는 실행할 액션을 선택하는 역할
◦ Q의 평가를 통해 결과가 좋았으면 강화하고, 결과가 안 좋았으면 약화하는 방식으로 학습 - 크리틱(critic): $Q_{w}$는 선택된 액션 $a$의 밸류를 평가하는 역할
◦ 현재의 정책 함수 $\pi$의 가치를 학습하는 방향으로 업데이트
Q Actor-Critic pseudo code
- 정책, 액션-벨류 네트워크의 파라미터 $\theta$와 $w$ 초기화
- 상태 $s$를 초기화
- 액션 $a~\pi_{\theta}(a|s)$를 샘플링
- 스텝마다 다음을 반복
◦ $a$를 실행하여 보상 $r$과 다음 상태 $s'$을 얻음
◦ $\theta$ 업데이트: $\theta \gets \theta + \alpha \nabla_{\theta} \log \pi_{\theta} (s, a) * Q_w(s, a)$
◦ 액션 $a' ~ \pi(a'|s')$를 샘플링
◦ $w$ 업데이트: $w \gets w + \beta (r + \gamma Q_w (s', a') - Q_w(s, a)) \nabla_w Q_w(s, a)$
◦ $a \gets a', s \gets s'$
◈ 어드밴티지 액터-크리틱
- Policy gradient 수식
◦ $\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * Q_{\pi_{\theta}} (s, a) \right ]$ - 가정
◦ 상태 $s'$이 너무 좋은 상태이기 때문에 어떤 액션을 취하든 얻게 되는 리턴이 높은 상황
◦ 예) $Q(s', a_0) = 1000, Q(s', a_1) = 1050$
◦ 이 둘의 차이를 학습하기 위해서는 무수히 많은 샘플이 필요할 수 있음
$$\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * \{Q_{\pi_{\theta}} (s, a) -V_{\pi_{\theta}}(s)\} \right ]$$
- 위 수식은 $s'$의 밸류가 업데이트의 양상에 영향을 주는 문제 해결
- 어드밴티지(advantage): $A_{\pi_{\theta}}(s, a) \equiv Q_{\pi_{\theta}(s, a) - V_{\pi_{\theta}}}(s)$
◦ 액션 $a$를 실행함으로써 "추가로" 얼마의 가치를 더 얻게 되느냐 하는 것
◦ $V_{\pi_{\theta}}(s)$ 를 기저(baseline)라고 함
$$\begin{equation}
\begin{split}
\mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * Q_{\pi_{\theta}} (s, a) \right ] &= \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * \{Q_{\pi_{\theta}} (s, a) -V_{\pi_{\theta}}(s)\} \right ] \\
&= \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * Q_{\pi_{\theta}} (s, a) \right ] - \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * V_{\pi_{\theta}} (s) \right ] \\
\text{즉},&\;\;\;\; \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * V_{\pi_{\theta}} (s) \right ] = 0 \\
\end{split}
\end{equation}$$
◈ 증명
- 상태 $s$에 대한 임의의 함수 $B(s)$에 대해서 다음이 성립
$\mathbb{E} \left [ \nabla_{\theta} \log \pi_{\theta} (s, a) * B(s) \right ] = 0$
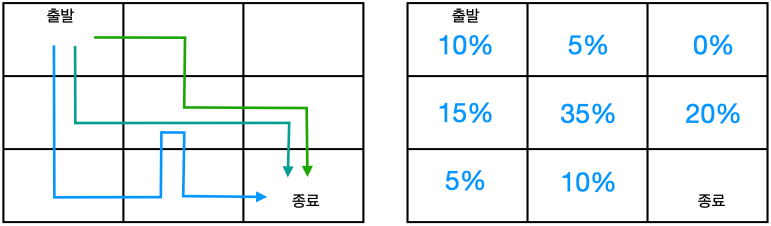
- 위 그림은 정책 $\pi$를 이용해 경로를 3번 탐색한 결과와 그에 따른 상태 분포 $d_{\pi}(s)$
- 상태 분포(state distribution): 각 상태의 방문 빈도를 나타내는 함수 $d_{\pi}(s)$
$$\mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * B(s) \right ] = \sum_{s \in S} d_{\pi_{\theta}}(s) \sum_{a \in A} \pi_{\theta}(s, a) \nabla_{\theta} \log \pi_{\theta} (s, a) * B(s)$$
- 기댓값 연산자를 풀어서 쓰면
$$\begin{equation}
\begin{split}
\sum_{s \in S} d_{\pi_{\theta}}(s) \sum_{a \in A} \pi_{\theta}(s, a) \nabla_{\theta} \log \pi_{\theta} (s, a) * B(s) &= \sum_{s \in S} d_{\pi_{\theta}}(s) \sum_{a \in A} \pi_{\theta}(s, a) {\nabla_{\theta}\pi_{\theta}(s, a) \over \pi_{\theta}(s, a)} * B(s) \\
&= \sum_{s \in S} d_{\pi_{\theta}}(s) \sum_{a \in A} \nabla_{\theta}\pi_{\theta}(s, a) * B(s) \\
&= \sum_{s \in S} d_{\pi_{\theta}}(s)B(s) \sum_{a \in A} \nabla_{\theta}\pi_{\theta}(s, a) \\
&= \sum_{s \in S} d_{\pi_{\theta}}(s)B(s) \nabla_{\theta} \sum_{a \in A} \pi_{\theta}(s, a) \\
&= \sum_{s \in S} d_{\pi_{\theta}}(s)B(s) \nabla_{\theta} 1 = 0 \\
\end{split}
\end{equation}$$
$$\therefore \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * B(s) \right ] = 0$$
- 기댓값 연산자 안에서 $V_{\pi_{\theta}}$를 빼도 기댓값이 변하지 않음
$$\begin{equation}
\begin{split}
\nabla_{\theta}J(\theta) &= \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * A_{\pi_{\theta}}(s, a) \right ] \\
A_{\pi_{\theta}}(s, a) &= Q_{\pi_{\theta}}(s, a) - V_{\pi_{\theta}}(s)
\end{split}
\end{equation}$$
- 위 수식은 어드밴티지 액터-크리틱의 policy gradient 수식
- 다음과 같은 3개의 뉴럴넷이 필요함
◦ 정책 함수 $\pi_{\theta}(s, a)$의 뉴럴넷 $\theta$
◦ 액션-가치 함수 $Q_w(s, a)$의 뉴럴넷 $w$
◦ 가치 함수 $V_{\phi}(s)$의 뉴럴넷 $\phi$
어드밴티지 Actor-Critic pseudo code
- 3쌍의 네트워크 파라미터 $\theta, w, \phi$를 초기화
- 상태 $s$를 초기화
- 액션 $a ~ \pi_{\theta}(a|s)$를 샘플링
- 스텝마다 다음을 반복
◦ $a$를 실행하여 보상 $r$과 다음 상태 $s'$을 얻음
◦ $\theta$ 업데이트: $\theta \gets \theta + \alpha_1 \nabla_{\theta} \log \pi_{\theta} (s, a) * \{ Q_w(s, a) - V_{\psi}(s) \}$
◦ 액션 $a' ~ \pi_{\theta}(a' | s)$를 샘플링
◦ $w$ 업데이트: $w \gets w + \alpha_2 (r + \gamma Q_w(s', a') - Q_w(s, a)) \nabla_wQ_w(s, a)$
◦ $\phi$ 업데이트: $\phi \gets \phi + \alpha_3 (r + \gamma V_{\phi}(s') - V_{\phi}(s)) \nabla_{\phi}V_{\phi}(s)$
◦ $a \gets a', s \gets s'$
◈ TD 액터-크리틱
- 가치 함수 $V(s)$의 TD 에러 $\delta$
$\delta = r + \gamma V(s') - V(s)$
$$\begin{equation}
\begin{split}
\mathbb{E}_{\pi}[\delta|s, a] &= \mathbb{E}_{\pi} \left [ r + \gamma V(s') - V(s)|s, a \right ] \\
&= \mathbb{E}_{\pi} \left [ r + \gamma V(s')|s, a \right ] - V(s) \\
&= Q(s, a) - V(s) = A(s, a)\\
\end{split}
\end{equation}$$
- 위 수식은 상태 $s$에서 액션 $a$를 실행했을 때 $\delta$의 기댓값
- $\delta$는 $A(s, a)$의 불편 추정량(unbiased estimate)
◦ $A(s, a)$ 대신 $\delta$를 이용해 업데이트해도 괜찮음 - 기존 어드벤티지 액터-크리틱에서의 policy gradient 수식을 다음과 같이 변형 가능
◦ $\nabla_{\theta}J(\theta) = \mathbb{E}_{\pi_{\theta}} \left [ \nabla_{\theta} \log \pi_{\theta}(s, a) * \delta \right ]$
TD Actor-Critic pseudo code
- 정책, 밸류 네트워크의 파라미터 $\theta$와 $\phi$를 초기화
- 액션 $a ~ \pi_{\theta}(a|s)$를 샘플링
- 스텝마다 다음을 반복
◦ $a$를 실행하여 보상 $r$과 다음 상태 $s'$을 얻음
◦ $\delta$를 계산: $\delta \gets r + \gamma V_{\phi}(s') - V_{\phi}(s)$
◦ $\theta$ 업데이트: $\theta \gets \theta + \alpha_1 \nabla_{\theta} \log \pi_{\theta} (s, a) * \delta$
◦ $\phi$ 업데이트: $\phi \gets \phi + \alpha_2 \delta \nabla_{\phi}V_{\phi}(s)$
◦ $a \gets a', s \gets s'$
◈ TD Actor-Critic 구현
- 이 부분은 구현에 대한 코드가 설명되어 있습니다.
'강화 학습 > 바닥부터 배우는 강화 학습' 카테고리의 다른 글
| 바닥부터 배우는 강화 학습 | 10. 알파고와 MCTS (0) | 2023.03.22 |
|---|---|
| 바닥부터 배우는 강화 학습 | 08. 가치 기반 에이전트 (0) | 2023.01.21 |
| 바닥부터 배우는 강화 학습 | 07. Deep RL 첫 걸음 (0) | 2023.01.17 |
| 바닥부터 배우는 강화 학습 | 06. MDP를 모를 때 최고의 정책 찾기 (0) | 2023.01.05 |
| 바닥부터 배우는 강화 학습 | 05. MDP를 모를 때 밸류 평가하기 (0) | 2022.11.29 |